💥 Level Set Collision
✅ 레벨 셋 충돌이란, 레벨 셋 기법을 사용하여 충돌 여부를 판단하는 방법이다.
➡️ 이때, 레벨 셋 기법은 경계면이 이동할 때 수치적인 기법을 통해 경계면을 추적하는 방법이다.
🔎 충돌 감지 (Collision Detection)
표면으로부터의 수직 거리를 나타내는 PI 값의 부호를 이용해 충돌 여부를 판단한다.
🎯 2차원에서의 반지름 2를 가지는 원을 예시로 다음과 같다:
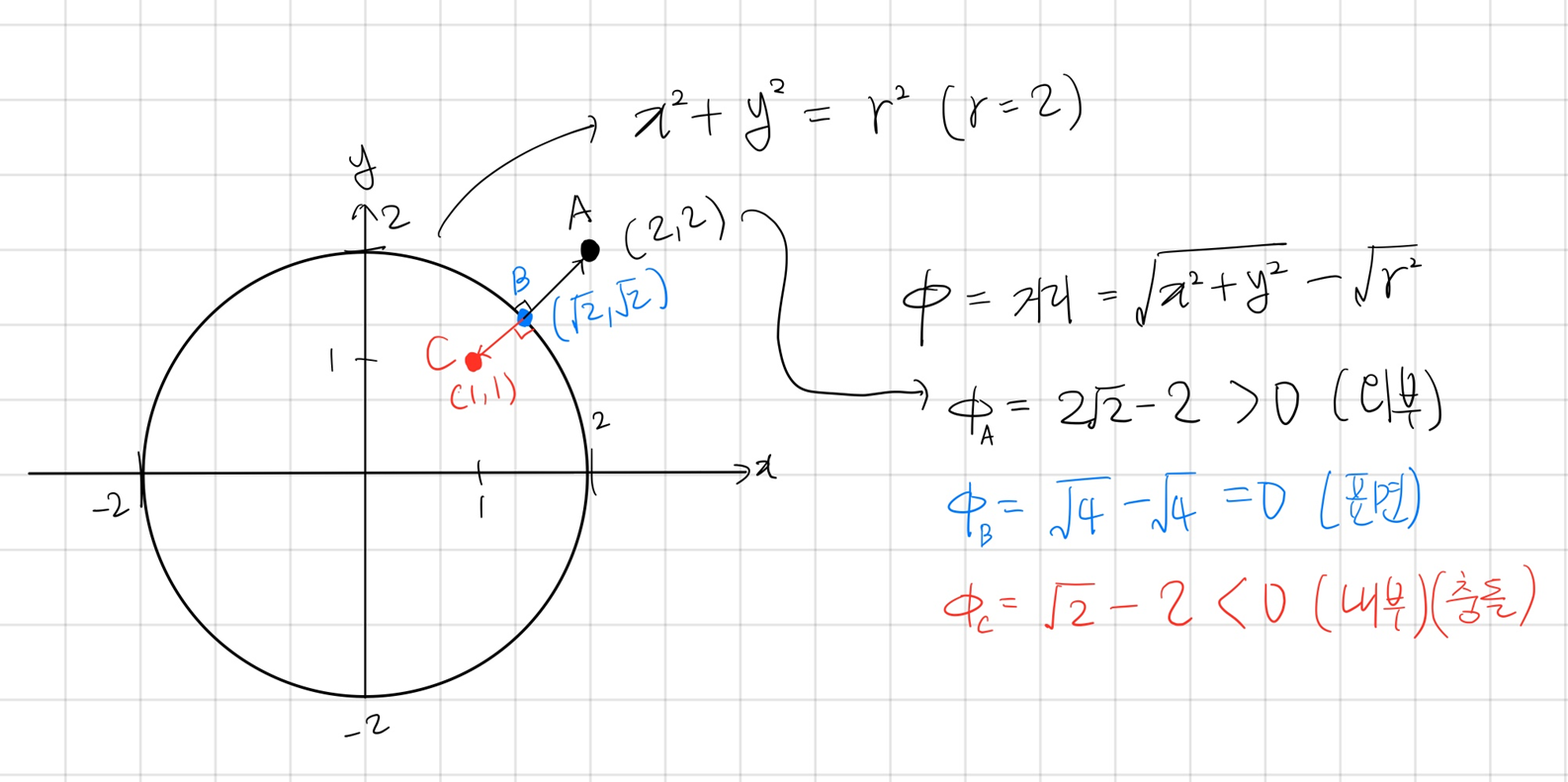
위의 그림에서, 각 점 A, B, C는 원의 외부, 표면, 내부에 위치해 있다.
이때, 각 점의 $\phi$ 값을 계산해 보면, A는 양수, B는 0, C는 음수 값을 가지는 것을 확인할 수 있다.
이를 통해 $\phi$ 값이 음수일 경우에 충돌을 의미한다는 것을 알 수 있다.
📏 표면으로부터의 수직 거리 ($\phi^{new}$)
충돌 여부를 한 단계 앞서 판단하기 위해 충돌 법선 방향의 상대 속도를 이용해 $\Delta t$ 시간 뒤의 표면으로부터 수직 거리 $\phi^{new}$ 를 계산하여 충돌 여부를 판단한다.
이때, $\phi^{new}$ 는 다음과 같이 계산할 수 있다:
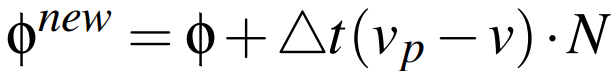
이처럼 상대 속도를 충돌 법선 방향으로 투영하여 수직 거리를 계산하며, 충돌 법선 벡터는 다음과 같이 $\nabla \phi$ 로 계산할 수 있다:

이때 $\nabla \phi$ 는 다음과 같이 오일러 방법이나 미분을 통해 값을 얻을 수 있다:


📃 Gradient PI ( $\nabla \phi$ )의 보충 설명
다음 그림은 $\nabla \phi$ 값을 원을 가정한 상황해서 구한 것이다.
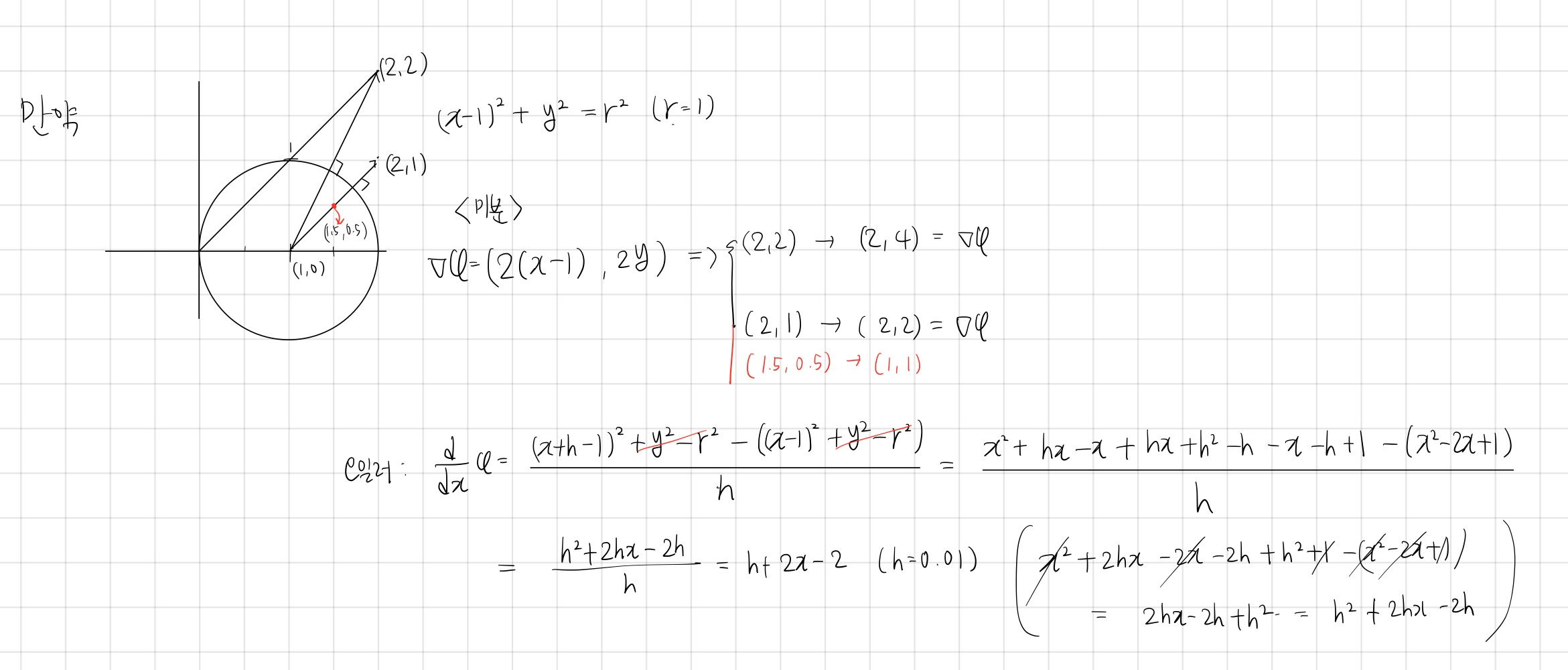

➡️ 이를 통해 $\nabla \phi$ 값이 현재 지점에서 원의 표면으로부터 가장 멀어질 수 있는 방향을 나타내는 것을 알 수 있다.
또한, 다음과 같이 속도를 이용해 $\Delta t$ 시간 뒤의 A의 다음 위치 A'을 계산했고, 표면으로부터 A'까지의 거리와 $\phi^{new}$ 값을 비교했다.
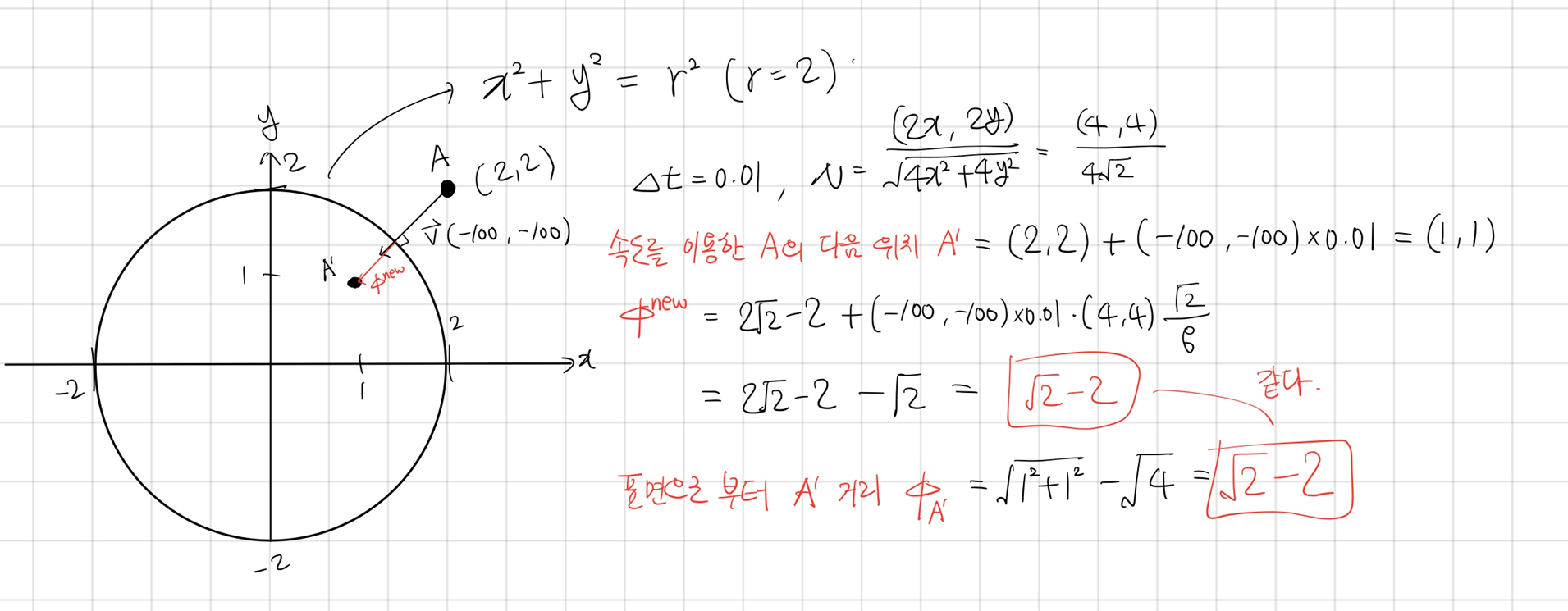
➡️ 이를 통해 $\phi^{new}$ 값과 A'과 표면 사이의 수직 거리 값이 같음을 확인할 수 있었다.
또한, $\phi^{new}$ 값을 계산할 때, 상대 속도를 충돌 법선 방향으로 투영했기 때문에, 만약 A가 표면과 수직이 아닌 속도 벡터를 가질 경우, 표면-A' 변위의 수직 방향 성분 크기와 $\phi$ 값이 같을 것임을 예상할 수 있다.
➡️ 따라서, 최종적으로 $\phi^{new}$ 값의 부호가 음수일 경우 충돌 처리를 해주는 것을 알 수 있다.
⚙️ 충돌 반응 (Collision Response)
충돌 처리를 위해 충돌 물체의 속도와 정점의 속도를 충돌 법선 방향과 충돌 접선 방향으로 나눈다.
이는 다음과 같이 나타낼 수 있다:

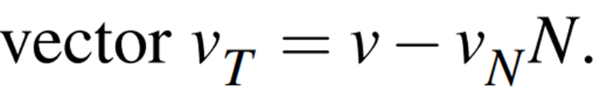
원래의 속도를 N 방향으로 투영하여 법선 방향 크기를 계산한 뒤, 이를 벡터 N과 다시 내적하여 법선 방향 속도를 원래의 속도에서 빼주면 접선 방향 속도를 구할 수 있다.
따라서, 정점의 새로운 속도는 다음과 같이 새로운 법선 방향 속도와 새로운 접선 방향 속도의 합으로 표현할 수 있다:

🚆 새로운 법선 방향 속력 $v^{new}_{p,N}$
먼저, 새로운 법선 방향 속력 $v^{new}_{p,N}$ 는 다음과 같이 나타낼 수 있다:
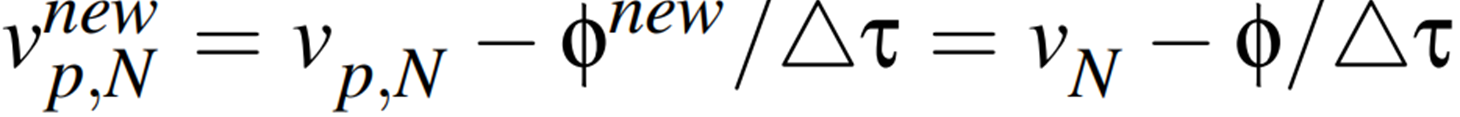
- 가운데의 식은 정점의 충돌 수직 방향 속력에서 표면으로부터의 수직 거리 즉, 표면으로부터 다음 위치까지의 수직 방향 변위를 시간 단계 델타 타우로 나누어 뺀 값이다.
- 오른쪽의 식은 가운데의 식의 $\phi^{new}$ 를 풀어쓴 것이다.
이러한 과정을 거쳐 법선 방향 속력을 조정한다면, 충돌 물체의 표면에 다음 위치가 머무르는 것을 다음에서 확인할 수 있다:

🚄 새로운 접선 방향 속력 $v^{new}_{p,T}$
정점의 새로운 접선 방향 속도는 상대 속도와 마찰력을 고려하여 나타낼 수 있다:
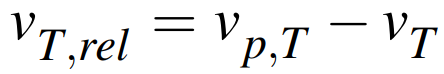
먼저, 상대 속도는 위와 같이 충돌 물체의 접선 방향 속도와 정점의 접선 방향 속도의 차이로 표현된다.
➡️ 따라서, 정점의 새로운 접선 방향 속도는 아래와 같이 새로운 접선 방향 상대 속도와 충돌 물체의 접선 방향 속도의 합으로 표현할 수 있다.
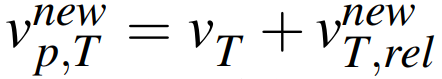
또한, 새로운 접선 방향 상대 속도는 다음과 같이 마찰력을 고려하여 나타낸다:
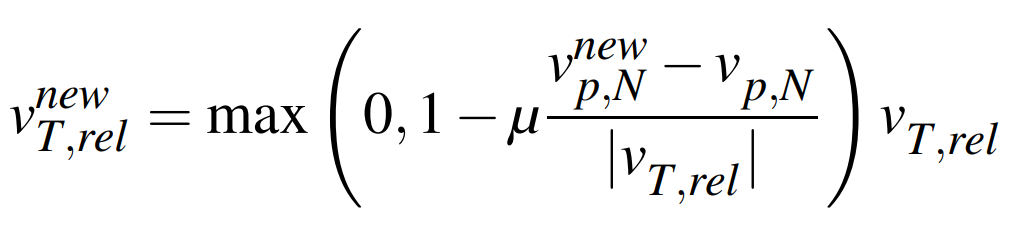
이 식은 아래와 같이 상대속도 - (수직 속력 전후 차이)*마찰계수*상대 속도 방향벡터로 나타낼 수 있다:

또한, 다양한 조건을 추가하여 식을 간단하게 수정할 수 있다. 만약, 충돌 물체가 정지 상태이고, 마찰이 없다면 새로운 접선 방향 상대 속도는 정점의 접선 방향 속도로 유지된다.
최종적으로 모든 계산 과정을 거친다면 다음과 같은 결과를 얻을 수 있다.
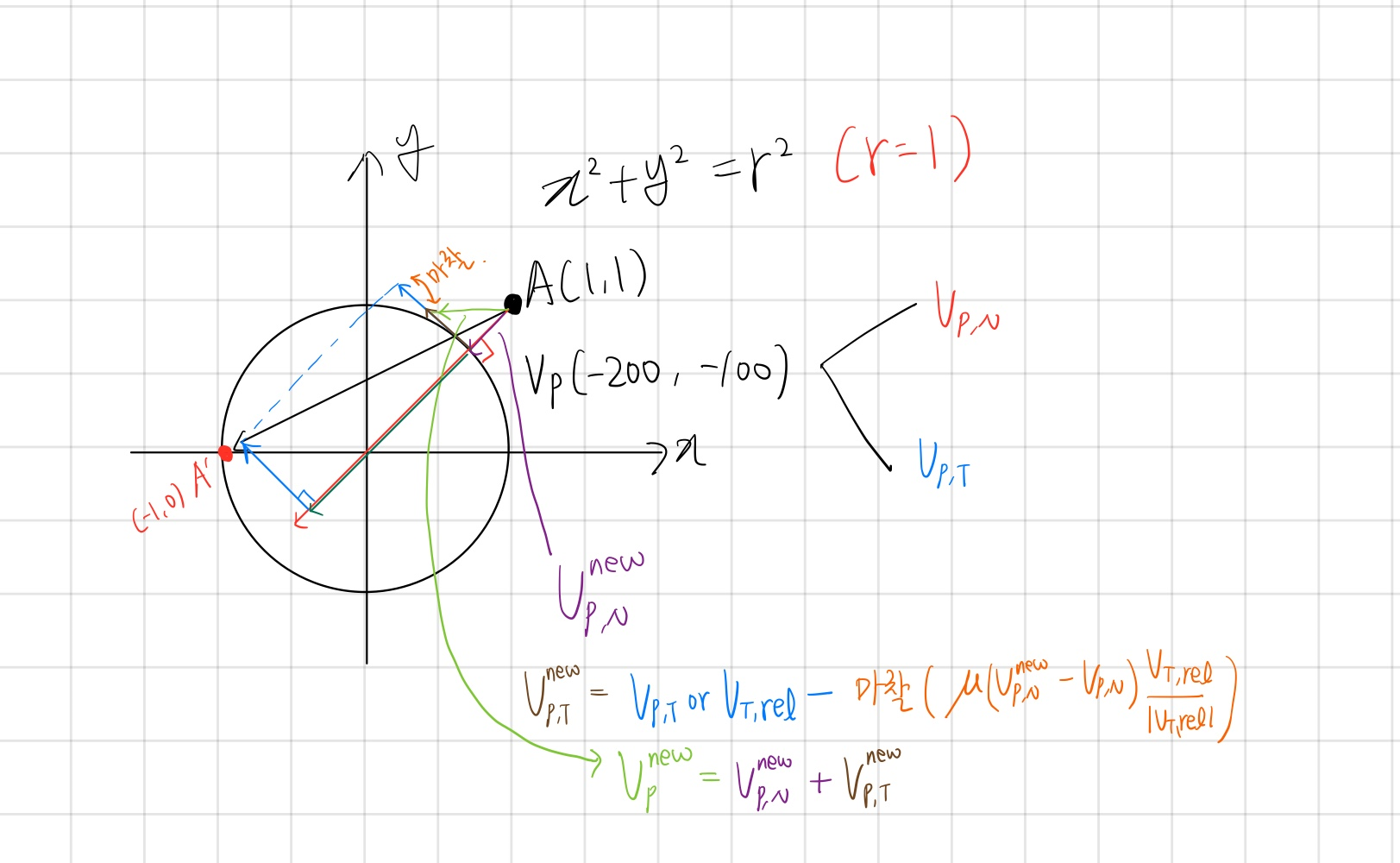
먼저, 구는 정지 상태이다. 또한, 정점 A의 속도를 충돌 법선 방향과 접선 방향으로 나눈 뒤, 법선 방향 속도에서 A의 새로운 위치 A'와 표면까지의 수직 방향 변위만큼을 빼서 새로운 법선 방향 속도를 계산한다.
다음으로, 새로운 접선 방향 속도를 계산하기 위해 접선 방향 속도에서 마찰력을 빼준다.
최종적으로 각각의 새로운 속도를 합하여 정점의 새로운 속도를 계산해 준다.
💻 구현 (Implement)
기존의 PBD 기반 천 시뮬레이션을 구현했던 코드에 다음과 같은 함수를 추가하여 구현했다.
void PBD_PlaneCloth::LevelSetCollision(void) //구는 정지 상태
{
double r = 1; //충돌 구체 반지름
double deltaT = 0.01f;
double h = 0.1f;
double coefficientFriction = 0.0f; //마찰 계수
for (int i = 0; i < _res[0]; i++) { //width
for (int j = 0; j < _res[1]; j++) { //height 모든 정점에 대하여 실행
int index = j * _res[0] + i;
double x = _pos[index].x();
double y = _pos[index].y();
double z = _pos[index].z();
vec3 N(calPI(x+h, y, z, r) - calPI(x, y, z, r),
calPI(x, y + h, z, r) - calPI(x, y, z, r),
calPI(x, y, z + h, r) - calPI(x, y, z, r));
N /= h; //법선 벡터 계산 (오일러 방법 이용) = Gradient PI
N.normalize();
double PI = calPI(x, y, z, r); //PI, newPI 계산
double newPI = PI + (_vel[index] * deltaT).dot(N);
if (newPI < 0)
{
double vpN = _vel[index].dot(N); //원래의 법선 방향 속력
vec3 vpNN = N * vpN; //원래의 법선 방향 속도
vec3 vpT = _vel[index] - vpNN; //원래의 접선 방향 속도
double newVpN = vpN - (newPI / deltaT); //새로운 법선 방향 속력
vec3 newVpNN = N * newVpN; // 새로운 법선 방향 속도
double friction = (coefficientFriction * (newVpN - vpN) / vpT.getNorm());
vec3 newVpT = vpT * (1 - friction);
if (1 - friction < 0)
newVpT.set(0, 0, 0);
_vel[index] = newVpNN + newVpT; //속도 업데이트
}
}
}
}
double PBD_PlaneCloth::calPI(double x, double y, double z, double r)
{
return sqrt(pow(x , 2) + pow(y + 1.5f, 2) + pow(z - 1, 2)) - r; //구 방정식
}이는 위에서 설명했던 과정을 단순히 코드로 구현한 것이므로 추가적인 설명은 생략한다.
최종적으로 각 정점의 속도를 업데이트하여 구현하였다.
📈 결과 (Result)
위의 결과는 각각 마찰 계수가 0일 때와 0.9일 때이다. 또한, 외력(바람)의 영향을 받을 때, 위치가 불안정적인 결과를 보이는 것을 확인할 수 있다.
참고 자료 :
Simulation of Clothing with Folds and Wrinkles - R. Bridson, S. Marino, R. Fedkiw
깃허브:
https://github.com/qkrdmstn/pbd-cloth-simulation.git
GitHub - qkrdmstn/pbd-cloth-simulation
Contribute to qkrdmstn/pbd-cloth-simulation development by creating an account on GitHub.
github.com
'물리 기반 시뮬레이션 > Cloth Simulation' 카테고리의 다른 글
| [ Cloth Simulation & Collision ] 06. SDF 생성 (0) | 2025.05.15 |
|---|---|
| [ Cloth Simulation & Collision ] 05. Local Optimization for SDF (0) | 2024.01.17 |
| [ Cloth Simulation & Collision ] 04. 천 자가 충돌 (Cloth Self-Collision) (0) | 2023.09.06 |
| [ Cloth Simulation & Collision ] 03. 충돌 (History-Based Collisions) (0) | 2023.07.19 |
| [ Cloth Simulation & Collision ] 01. 천 시뮬레이션 (Cloth Simulation) (0) | 2023.07.06 |
