📌 미분 방정식이란?
알려지지 않은 함수와 그 미분 사이의 관계를 설명하는 방정식이다.
미분 방정식은 일반적으로 다음과 같이 정의된다.
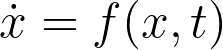
미분 방정식의 해를 구하는 것은 위의 관계를 만족시키는 함수를 찾는 것을 의미한다.
이는 아래에 있는 2차원에서의 벡터장과 같이 도함수 $f$ 를 구하는 과정이다.

2차원에서 도함수 $f$ 는 평면상의 벡터장을 나타내고, $x$ 에서의 벡터는 점 $p$ 가 $x$ 를 지날 때 가져야 하는 속도를 나타낸다.
➡️ 따라서, 초기 값을 지정하면 모든 미래의 운동은 함수 $f$ 에 따라 달라진다.
🧩 초기 값 문제 ( Initial Value Problem )
초기 값 문제는 미분 방정식을 통해 얻은 벡터장에 초기 값을 지정할 경우, 다음 운동이 함수 $f$ 에 의해 결정된다는 개념이다. 이는 아래와 같은 그림을 통해 시각적으로 확인할 수 있다:

⚠️ 만약, 도함수 $f$ 가 매개변수 시간 $t$ 에 의해 영향을 받는 함수라면, 다음과 같이 $t$ 에 이중적으로 영향을 받는다.
✔️ 도함수 $f$ 의 벡터장이 시간 $t$ 에 따라 변화한다.
✔️ 점 $p$ 는 $x(t)$ 에 따라 경로를 이동한다.
❗ 이중 시간 의존성은 혼란을 유발하므로 주의가 필요하다.
🔢 수치해석 ( Numerical Analysis )
✅ 초급 미분 방정식은 미지 함수의 기능적 형태를 추측하는 기호적인 해를 중점으로 다룬다.
❗ 하지만, 물리 기반 시뮬레이션에서는 숫자적인 해에 관심이 있다.
📌 때로는 해석해를 계산하는 것이 복잡하고 비효율적이기 때문에 우리는 수치적 방법을 통해 근사값(수치해)을 구한다.
수치적 접근은 다음과 같다:
✔️ 이산적(불연속적)인 시간 단계를 거쳐 진행
✔️ 각 시간 단계마다 도함수를 계산
대표적인 방법으로는 오일러 방법(Eluer's Method)과 중간점 방법(Midpoint Method)이 있다.
🧮 오일러 방법 ( Eluer's Method )

✅ 가장 간단한 수치 해법이며, 초기 값 $x$ 를 $x_0 = x(t_0)$ 라 표기하고 나중 시간 $t_0 + h$ 에서의 예상 값을 $x(t_0 + h)$ 라 한다.
- $h$ 는 Step Size 매개변수
- 도함수 벡터장 방향으로 한 단계 진행하여 $x(t_0 + h)$를 계산
이는 다음 이론들로부터 유도된다:
- 📘 미분의 정의

- 🧾 테일러 급수 (Talyor Series)

오일러 방법은 테일러 급수에서 제외한 고차항만큼 오차가 발생한다. ($O(h^2)$ -> $h$ 에 비례)
특징:
1. 계산된 값을 통해 다음 단계의 값을 계산하기 때문에 오차가 누적된다.
2. 특정 조건을 만족하지 않을 경우 발산하는 특징을 가진다.
이는 아래의 그림에서도 확인할 수 있다.

📌 $h$ 를 절반으로 줄이면 오차는 오차는 $1/4$ 만큼 줄어든다.
👉 하지만, 2배 더 많은 계산이 필요하다.
🧮 중간점 방법 ( Midpoint Method )

✅ 수정된 오일러 방법 및 2차 Runge-Kutta 방법이라고 한다.
➡️ 오차가 $O(h^3)$ 인 대신 계산량이 증가했다.
이는 오일러 단계를 실행하는 과정에서 그다음 단계에서의 중점에서 도함수 $f "$(2번 미분) 를 계산하여 $x$를 업데이트 한다.
📈 이를 더 고차로 발전시키면:
➡️ 가장 많이 쓰이는 4차 Runge-Kutta 방법, 이는 $O(h^5)$의 오차를 가진다.
⚙️ 적응형 단계 크기 ( Adaptive Stepsizes )
📌 위의 어떤 방법을 사용하더라도 좋은 Step Size를 결정하는 것은 주요 문제이다.
✅ 따라서, 이 문제의 목표는 오차가 원하는 범위 내에 있으면서, $h$ 값을 최대화하는 것이다.
➡️ 오차가 작으면 $h$ 를 키우고, 오차가 커지면 $h$를 줄이는 Adpative Stepsizing을 적용한다.
💻 구현 (Implementation)
코드의 재사용성을 높이기 위해 ODE Solver와 모델을 서로 독립적으로 구현한다.
📐 ODE Solver
미분 방정식의 해를 근사적으로 계산하기 위한 계산 알고리즘이다. 위에서 소개한 오일러 방법, 중간점 방법 등을 사용할 수 있다.
이는 두 가지 방법이 있다:
✔️ 명시적 방법 (Explicit): 현재 값 기준으로 계산
✔️ 암시적 방법 (Implicit): 대수 방정식 해결 후 미래 값 계산
또한, ODE Solver는 다음과 같은 기능들을 수행한다:
✔️ $dim(x)$의 반환
✔️ $x$ 와 $t$의 $get/set$
✔️ 현재 $x$와 $t$ 값으로 미분 계산
🧪 Model
✅ 물리적 시스템을 수학적으로 나타낸다.
➡️ 이는 시스템의 동작을 결정하는 기본 원리, 법칙, 가정 등을 표현한다.
예시: 입자 시스템에서는 입자들의 질량, 위치, 속도, 그들에게 작용하는 힘을 표현한다.
참고 자료 :
https://graphics.pixar.com/pbm2001/
오일러 방법 :
https://angeloyeo.github.io/2021/04/30/direction_fields.html
https://blog.naver.com/mykepzzang/220601629315
테일러 급수 :
https://mathpeak.tistory.com/371
https://darkpgmr.tistory.com/59
중간점 방법 :
https://www.wikiwand.com/ko/중간점_방법
'물리 기반 시뮬레이션 > 기초' 카테고리의 다른 글
| [ 물리 기반 시뮬레이션 ] 03. 위치 기반 역학 (Position Based Dynamics) (0) | 2023.07.03 |
|---|---|
| [ 물리 기반 시뮬레이션 ] 02. 입자 역학 (Particle Dynamics) (0) | 2023.06.22 |