[ 물리 기반 시뮬레이션 ] 02. 입자 역학 (Particle Dynamics)

📌 입자란?

입자는 질량, 위치, 속도를 가지며 힘에 영향을 받고, 공간적으로 확장되지 않는 개체이다.

이는 단순하기 때문에 시뮬레이션하기 가장 쉽고, Damped Spring으로 연결하는 등 간단하지만 다양하고 흥미로운 동작을 보일 수 있다.

🌌 위상공간 (Phase space)

위상공간은 수리물리학에서 계가 가질 수 있는 모든 상태로 이루어진 공간이다.

➡️ 한 입자의 상태는 위치와 속도(또는 운동량)으로 정해진다. -> 총 6차원(= 공간 3차원 * 변수 2개)

🎯 예시:

뉴턴의 입자 운동은 $f = ma$ 또는 $x" = f/m$에 의해 결정된다. 이는 2계 도함수를 포함하기 때문에 속도를 나타내는 변수 $v$ 를 생성하여 결합된 1차 ODE 형태로 만들 수 있다:

이때 위치와 속도 $x$ 와 $v$ 는 6차원 벡터를 형성한다. 이 위치/속도 공간을 위상공간(Phase space)라고 한다.

구성 요소로 $[x'_1, x'_2, x'_3, v'_1, v'_2, v'_3] = [v_1, v_2, v_3, f_1/m, f_2/m, f_3/m]$ 가 있고, $n$ 개의 입자로 구성된 시스템은 이러한 방정식의 $n$개의 사본을 붙여 $6n$의 길이를 형성한다.

🛠️ 기본 입자 시스템 (Basic Particle Systems)

입자 시스템을 구현할 때, 모델의 두 가지 관점을 유지해야 한다:

1. ODE Solver(외부)의 관점에서, 모델은 단일체로 보여야 한다.

2. 내부의 관점에서, 모델은 구조화된 형태 + 서로 다른 객체의 집합으로 표현돼야 한다.

구조체 정의 (C 언어)

// 입자
typedef struct{
	float m; /* 질량 */
	float x[3]; /* 위치 벡터 */
	float v[3]; /* 속도 벡터 */
	float f[3]; /* 힘 누적기 */
} *Particle;

// 입자 시스템
typedef struct{
	Particle p; /* 입자 포인터 배열 */
	int n; /* 입자의 개수 */
	float t; /* 시뮬레이션 시간 */
} *ParticleSystem;

📐 ODE Solver에 포함되는 연산

/* 상태 도함수 및 힘 벡터의 길이 */
int ParticleDims(ParticleSystem p){
	return (6 * p->n);
};

/* 입자에서 상태를 dst로 수집 */
int ParticleGetState(ParticleSystem p, float *dst){
	int i;
	for(i=0; i < p->n; i++){
		*(dst++) = p->p[i]->x[0];
		*(dst++) = p->p[i]->x[1];
		*(dst++) = p->p[i]->x[2];
		*(dst++) = p->p[i]->v[0];
		*(dst++) = p->p[i]->v[1];
		*(dst++) = p->p[i]->v[2];
	}
}

/* src에서 상태를 입자로 분산 */
int ParticleSetState(ParticleSystem p, float *src){
	int i;
	for(i=0; i < p->n; i++){
		p->p[i]->x[0] = *(src++);
		p->p[i]->x[1] = *(src++);
		p->p[i]->x[2] = *(src++);
		p->p[i]->v[0] = *(src++);
		p->p[i]->v[1] = *(src++);
		p->p[i]->v[2] = *(src++);
	}
}

/* 도함수를 계산하고 dst에 배치 */
int ParticleDerivative(ParticleSystem p, float dst){
	int i;
	Clear_Forces(p); /* 힘 누적기를 0으로 초기화 */
	Compute_Forces(p); /* 힘을 계산하는 함수 */
	for(i=0; i < p->n; i++){
		*(dst++) = p->p[i]->v[0]; /* xdot = v */
		*(dst++) = p->p[i]->v[1];
		*(dst++) = p->p[i]->v[2];
		*(dst++) = p->p[i]->f[0]/m; /* vdot = f/m */
		*(dst++) = p->p[i]->f[1]/m;
		*(dst++) = p->p[i]->f[2]/m;
	}
}

🌀 오일러 Solver (Euler Solver)

void EulerStep(ParticleSystem p, float DeltaT){
	ParticleDeriv(p,temp1); /* 각 입자의 상태로부터 도함수 얻기 */
	ScaleVector(temp1,DeltaT) /* 스케일링 */
	ParticleGetState(p,temp2); /* 각 입자의 현재 상태 얻기 */
	AddVectors(temp1,temp2,temp2); /* 더하기 -> temp2 */
	ParticleSetState(p,temp2); /*각 입자의 상태를 업데이트 */
	p->t += DeltaT; /* 시간 업데이트 */
}

💥 힘 (Forces)

모든 입자는 본질적으로 같지만, 힘을 생성하는 객체들은 각각 다르다.

➡️ 기본 입자 시스템 모델을 수정하지 않고 힘을 생성하는 객체의 집합을 확장하기 쉽게 만들어야 한다.

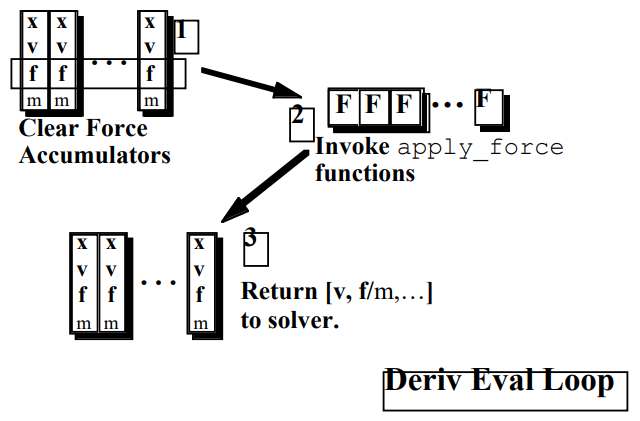
➡️ 각 힘 객체는 모든 입자에 접근하며, CalculateForces() 함수를 통해 ApplyForce() 함수를 호출한다.

📈 이 과정을 다음 그림에서 확인할 수 있다:

🧲 힘의 종류

힘은 크게 세 가지로 나눌 수 있다.

✔️ 단항 힘 (Unary forces) : 각 입자에 독립적으로 작용, 일정한 힘을 가하거나 입자 위치, 속도, 시간 중 하나 이상과 관련된 힘

✔️ n-항 힘 (n-nary forces) : 고정된 입자 집합에 힘을 가하는 힘

✔️ 공간 상호작용 힘(forces of spatial interaction) : 입자의 위치에 따라 모든 쌍의 입자에 영향을 미치는 힘

🔻 단항 힘 (Unary Forces)

중력 (Gravity)

각 입자에 작용하는 중력은 $f = mg$ 로 표현된다. 여기서 $g$ 는 일정한 크기와 방향을 가진 벡터(중력 상수)이다.

➡️ 모든 입자가 동일한 중력을 받기 위해, 입자 목록을 순회하며 각 입자의 힘 누적기에 적절한 힘을 추가한다.

📌 중력은 기본적으로 입자 시스템에 직접 연결될 수 있을 정도로 기본적인 개념이다.

점성 마찰 (Viscous Drag)

이상적인 점성 마찰은 $f= -kv$ 로 표현된다. 여기에서 $k$ 는 마찰 계수이다.

➡️ 마찰은 입자의 운동을 저항하여 입자가 서서히 정지하도록 만든다.

📌 숫자의 안정성을 향상하기 위해 각 입자에 약간의 마찰을 적용하는 것이 권장된다.

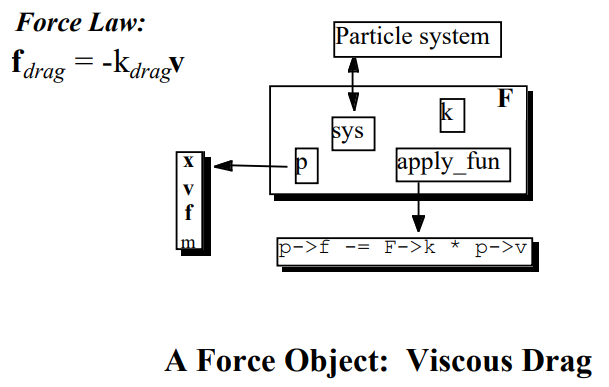
중력과 마찰 모두 시스템에 기본적으로 포함되어 구현될 수 있으며, 이를 다음과 같은 그림에서 확인할 수 있다:

🔗 n항 힘 (n-nary forces)

이진 힘 (Binary forces)의 대표적인 예로 훅의 법칙 (Hooke's law)이 있다.

위치 $a$ 와 $b$ 에 있는 두 입자 사이의 스프링 힘은 다음과 같다:

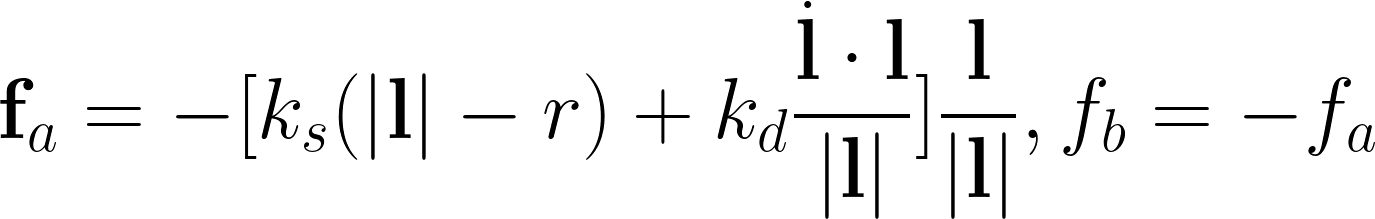
여기에서:

$f_a$ 와 $f_b$ 는 $a$ 와 $b$ 에 작용하는 힘
$I = a-b, r$ 은 잔여 길이
$k_s$ 는 스프링 상수
$k_d$ 는 감쇠 상수
$l'$ 은 $l$ 의 시간 미분으로, 두 입자의 속도 차이인 $v_a-v_b$ 와 같다.

➡️ 위의 식에서 스프링 힘의 크기는 실제 길이와 잔여 길이의 차이에 비례하고, 감쇠 힘의 크기는 $a$ 와 $b$ 의 접근 속도에 비례한다.

📌 Damped spring은 연결된 입자 쌍을 가리키는 구조체로 구현될 수 있다. 위의 식에 따라 힘을 적용하는 코드는 두 입자 구조체로부터 위치와 속도를 가져와 계산을 수행한 뒤, 결과를 입자의 힘 누적기에 합산한다.

힘 객체의 구조는 다음과 같다.

🌌 공간 상호작용 힘

모든 입자 쌍 사이에 작용하는 인력, 척력 등이 있다.

🧮 에너지 함수 (Energy Functions)

✅ 행동 함수는 사물이 특정 조건을 만족할 때 정확히 0이 되는 함수이다.

🎯 예시:

조건: 두 입자 $a$ 와 $b$ 가 동일한 위치에 존재

조건: 두 입자 $a$ 와 $b$ 가 거리 $r$ 만큼 떨어진 위치에 존재

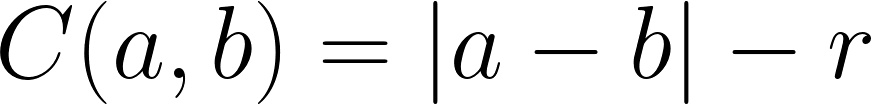
이러한 종류의 함수는 나중에 제약 조건 동역학을 공부할 때, 제약 조건을 지정하는 방법으로 사용할 수 있다.

✅ 행동 함수 $C(x_1,...,x_n)$를 힘 법칙으로 변환하는 과정은 다음과 같다:

스칼라 퍼텐셜 에너지 함수를 정의:

여기서 $k_s$ 는 일반화된 강성 계수이다.

스칼라 퍼텐셜의 힘은 에너지 그래디언트의 음수이므로, $C$ 에 대한 입자 $x_i$의 힘은 다음과 같다:

$C = 0$ 주변의 안정성을 위해 감쇠를 추가하면 힘 식은 다음과 같다:

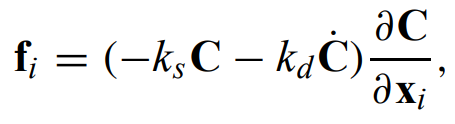
여기서 $k_d$ 는 일반적인 감쇠 상수이며, $C'$ 은 $C$ 의 시간 도함수이다.

$C'$ 를 계산할 때, $x'_i = v_i$를 이용하여, $C = x_1 - x_2, C' = v_1 - v_2$ 가 된다. 이를 위의 일반 식에 대입하면 다음과 같다:

이는 감쇠가 있는 스프링에 대한 힘 법칙이다.

🚧 입자/면 충돌과 접촉 (Particle/Plane Collisions and Contact)

일반적으로 충돌과 접촉 문제는 매우 어렵지만, 입자가 면(예: 지면이나 벽)과 충돌하는 경우는 가장 간단한 경우이다.

또, 충돌 문제에는 충돌 감지(Collision Detection)와 충돌에 대한 반응(Collision Response) 두 가지가 있다.

⚠️ 충돌 감지 (Collision Detection)

📌 $P$ 가 면 위의 한 점이고, $N$ 이 안쪽을 가리키는 법선이라면, 점 $X$ 가 면과 충돌했는지 판단하기 위해 $(X-P) \cdot N$ 의 부호를 확인한다.

양수: 안쪽
음수: 바깥
0: 접촉

💥 충돌 반응 (Collision Response)

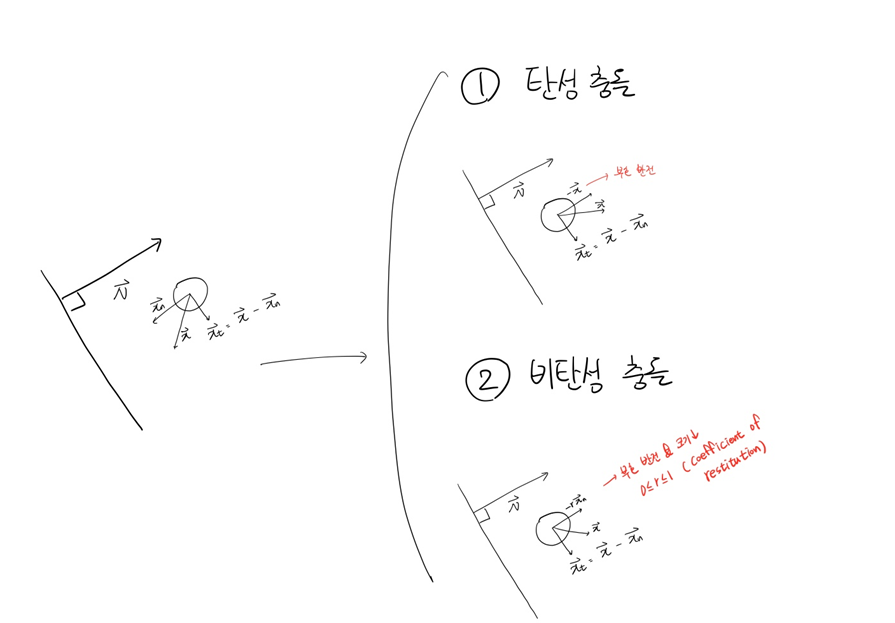
📌 충돌 반응을 설명하기 위해 속도와 힘 벡터를 충돌 면에 수직인 직교 성분과 그에 평행한 성분 두 개로 나눈다.

➡️ $N$ 이 충돌 면의 법선 벡터라면, 벡터 $x$ 의 수직 성분은 $x_n = (x \cdot N) N$ 이며, 접선 성분은 $x_t = x - x_n$ 이다.

✔️ 가장 간단한 충돌은 탄성 충돌이다. 마찰이 없기 때문에 입자의 수직 성분 속도의 부호를 반전시키면 된다.

✔️ 비탄성 충돌의 경우 수직 속도 성분에 상수인 $-r$ 을 곱한다. 여기서 $r$ 은 0과 1 사이의 복원 계수(coefficient of restitution) 이다. $r$ 이 0이라면 입자는 튕기지 않으며, 1이라면 매우 튕길 것이다.

🤝 접촉 (Contact)

✅ 입자가 충돌 면에 위치하여 수직 속도가 0이라면 접촉 중을 의미한다.

✅ 밀려날 경우: $(N·f < 0)$ 이면 수직 성분을 상쇄한다.

✅ 마찰력: 접선 방향으로 작용, 크기는 수직력에 비례한다:

참고 자료 :

https://graphics.pixar.com/pbm2001/

위상공간 :

https://ko.wikipedia.org/wiki/위상_공간_(물리학)

'물리 기반 시뮬레이션 > 기초' 카테고리의 다른 글

[ 물리 기반 시뮬레이션 ] 03. 위치 기반 역학 (Position Based Dynamics) (0)	2023.07.03
[ 물리 기반 시뮬레이션 ] 01. 미분 방정식 기초 (Differential Equation Basics) (0)	2023.06.21

📌 입자란?

🌌 위상공간 (Phase space)

🛠️ 기본 입자 시스템 (Basic Particle Systems)

구조체 정의 (C 언어)

📐 ODE Solver에 포함되는 연산

🌀 오일러 Solver (Euler Solver)

💥 힘 (Forces)

🧲 힘의 종류

🔻 단항 힘 (Unary Forces)

중력 (Gravity)

점성 마찰 (Viscous Drag)

🔗 n항 힘 (n-nary forces)

🌌 공간 상호작용 힘

🧮 에너지 함수 (Energy Functions)

🚧 입자/면 충돌과 접촉 (Particle/Plane Collisions and Contact)

⚠️ 충돌 감지 (Collision Detection)

💥 충돌 반응 (Collision Response)

🤝 접촉 (Contact)

'물리 기반 시뮬레이션 > 기초' 카테고리의 다른 글

티스토리툴바